最大公约数 (GCD) 是最大的正整数,也是给定正整数集合的公约数。它也被称为最大公因数(HCF)或最大公因数(GCF)。
一对正整数(a,b)的最大公约数定义为两个正整数的公因数(a,b)的最大正数。任何两个数的 GCD 永远不会是负数或零,因为任何两个数共享的最小正整数总是 1。
例如:让我们取两个数字 75 和 30,所以可以将这两个数字整除的最大数字将是 15。
解释:可以同时整除 75 和 30 的数字是 [1,3,5,15],所以其中最大的数字是 15,所以它将是 75 和 30 的 GCD。
示例 2:让我们取两个数字 128 和 32,因此可以将这两个数字整除的最大数字将是 32。
解释:能整除 128 和 32 的数是 [1,2,4,8,16,32],所以其中最大的数是 32,所以它将是 128 和 32 的 GCD。
计算C中两个数的GCD
我们可以从上面的例子中推断出可以同时整除两个数的最大数小于可以整除两个输入数的最小数。因此,我们可能会创建一个简单的方法,在该方法中,我们从两个整数之间的最小数字开始测试每个数字,然后一直到 1。结果,两个数字的 GCD将是任何先出现的数字并完全除以两个输入数字。
例子:
输入数字:N1 = 132 & N2 = 24
最小数:N2 = 24
我们将从 24 开始一个以 1 结束的循环。然后我们将找到第一个将数字 N1 和 N2 完全整除的数字,在本例中为 12。因此 N1 和 N2 的 GCD 将为 12。
上述查找GCD方法的算法:
- 声明两个变量 num1 和 num2。
- 初始化两个变量。
- 找到两个数字之间的最小数字并将其存储在不同的变量(minNum)中。
- 从 minNum 开始循环到 1。
- 现在检查 num1 和 num2 是否可以被当前迭代数整除,然后将其结果存储在另一个变量中并退出循环。如果它们不可分割,则继续相同的步骤。
- 打印结果。
上述算法的C程序
#include <stdio.h>
int main()
{
int num1, num2, i;
//Accepting and storing input of two numbers from user
printf("Enter two numbers: ");
scanf("%d ", &num1);
scanf("%d ", &num2);
int minNum=0;
int result = 1;
//Calculating smallest number among num1 and num2
if(num1<num2){
minNum = num1;
} else {
minNum = num2;
}
//loop from minNum to 1
for( i = minNum; i > 1; --i )
{
//check if both num1 and num2 is divisible by i or not
//store the outcome and break out of the loop
if(num1%i == 0 && num2%i == 0){
result = i;
break;
}
}
//Print the result
printf("GCD of %d and %d is %d", num1, num2, result);
return 0;
}
您可以在Interviewbit上运行此代码。
输入: 132、24
输出: 132 和 24 的 GCD 是 12。
解释: 132 和 24 中最小的数字是 24,所以循环从 24 开始,并检查 132 和 24 是否可被 24 整除,因为两者都不可整除,所以循环将继续运行,现在它将检查 23 等等直到循环达到 12,其中两个数字都可以被 12 整除,因此它将存储结果并跳出循环,然后打印结果。
时间复杂度:由于循环运行的最小数字(n)到1,所以时间复杂度为O(n)。
空间复杂度:除了一些与输入无关的变量之外,它不占用任何额外空间,因此该算法的空间复杂度将为 O(1)。
我们可以通过使用一种有效的方法来降低该算法的时间复杂度。
高效方法:欧几里得算法
以下事实是该算法的基础:
- 当我们从一个较大的数字中减去一个较小的数字(我们减少一个较大的数字)时,GCD 不会改变。因此,如果我们继续减去较大的两个值,我们会得到 GCD。
- 不是减法,而是除以较小的整数,当我们发现余数为 0 时,程序将终止。
我们可以首先确定 2 之间的最小整数并将该数字用作除数。最大的组成部分将是我们的股息。然后我们将它除以直到余数为零。如果余数超过零。
然后余数将成为除数,当前除数将成为被除数。并且必须重复直到余数为零。
示例:给定两个数字:N1=132,N2=24。
请参阅下图以更好地理解
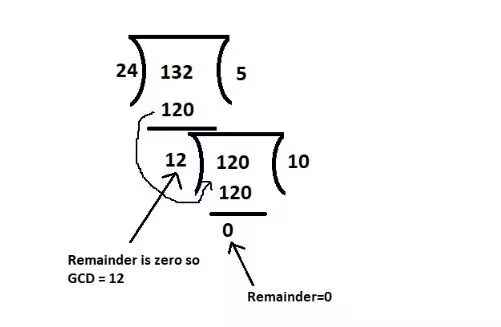
在上图中,我们对整数进行除数,直到我们得到残差为 0。当余数等于 0 时,当前除数就是 GCD。
这种方法的算法:
定义一个接受两个参数除数和除数的函数。
现在在函数中检查除数是否完全除除被除数。如果除数完全除,则返回除数。
通过提供除数作为除数和被除数的余数来递归调用该函数。除了股息作为当前的除数。
上述算法的C程序
#include <stdio.h>
//Function to calculate GCD
int gcd(int divisor, int dividend)
{
//Calculating remainder
int remainder = dividend % divisor;
//Base condition
//If remainder is 0 then divisor will be GCD
if(remainder == 0)
{
return divisor;
}
//Recursive call to find GCD
return gcd(remainder, divisor);
}
int main()
{
int num1, num2;
//Accepting and storing input of two numbers from user
printf("Enter two numbers: ");
scanf("%d ", &num1);
scanf("%d ", &num2);
int dividend, divisor;
//dividend will be the number which is gretest among the input
if(num1 > num2){
dividend = num1;
} else {
dividend = num2;
}
//Divisor will be the number which is lowest among the input
if(num1 < num2){
divisor = num1;
} else {
divisor = num2;
}
//Calling function to calculate GCD
int ans = gcd(divisor, dividend);
//Print the result
printf("GCD of %d and %d is %d", num1, num2, ans);
return 0;
}
您可以在Interviewbit上运行此代码。
输入: 132、24
输出: 132 和 24 的 GCD 是 12。
时间复杂度: O(log(min(num1,num2)),相当于 O(log(n))。
空间复杂度: O(1),除了一些变量之外没有使用额外的空间。
结论:
GCD(最大公约数)是一种数学工具,它指定可以同时除两个整数的数。我们已经看到了用于实现该算法的 Java 代码。我们还理解了算法的分析,以评估算法的优化程度。计算两个整数的 GCD 的最佳方法(欧几里德算法)显着降低了竞争性编程期间的复杂性。

