实现反向传播算法神经网络的 C++ 类,支持任意数量的层/神经元
介绍
该类CBackProp封装了一个前馈神经网络和一个反向传播算法来训练它。本文适用于那些已经对神经网络和反向传播算法有所了解的人。如果您不熟悉这些,我建议您先阅读一些材料。
背景
这是我在大学最后一个学期从事的一个学术项目的一部分,为此我需要找到隐藏层的最佳数量和大小以及不同数据集的学习参数。最终确定神经网络的数据结构并让反向传播算法发挥作用并不容易。本文的动机是为其他人节省同样的努力。
这里有一点免责声明… 本文描述了该算法的简单实现,并没有充分阐述该算法。包含的代码还有很大的改进空间(比如添加异常处理:-),对于许多步骤,需要的推理比我所包含的要多得多,例如,我为参数选择的值和数量层数/每层中的神经元用于演示用法,可能不是最佳的。要了解更多关于这些,我建议去:
- 神经网络常见问题解答
使用代码
通常,使用涉及以下步骤:
- 使用创建网络
CBackProp::CBackProp(int nl,int *sz,double b,double a) - 应用反向传播算法 – 通过
void CBackProp::bpgt(double *in,double *tgt)在循环中传递输入和所需输出来训练网络,直到由获得的均方误差CBackProp::double mse(double *tgt)减小到可接受的值。 - 使用经过训练的网络通过使用前馈输入数据来进行预测
void CBackProp::ffwd(double *in)。
以下是我所包含的示例程序的描述。
一步一步来…
设定目标
我们将尝试教我们的网络破解二进制A XOR B XOR C。XOR 是一个明显的选择,它不是线性可分的,因此需要隐藏层并且不能通过单一的感知来学习。
训练数据集由多条记录组成,其中每条记录包含输入到网络的字段,然后是包含所需输出的字段。在此示例中,它是三个输入 + 一个所需的输出。
// prepare XOR training data
double data[][4]={// I XOR I XOR I = O
//--------------------------------
0, 0, 0, 0,
0, 0, 1, 1,
0, 1, 0, 1,
0, 1, 1, 0,
1, 0, 0, 1,
1, 0, 1, 0,
1, 1, 0, 0,
1, 1, 1, 1 };
配置
接下来,我们需要为我们的神经网络指定一个合适的结构,即它应该具有的隐藏层数和每层中的神经元数。然后,我们为其他参数指定合适的值:学习率– beta,我们可能还想指定动量– alpha(这个是可选的)和阈值– thresh(目标均方误差,一旦达到,训练停止,否则继续num_iter数次)。
让我们定义一个有 4 层的网络,分别有 3、3、3 和 1 个神经元。由于第一层是输入层,即只是输入参数的占位符,它必须与输入参数的数量相同,最后一层作为输出层的大小必须与输出的数量相同- 在我们的示例中,它们是 3 和 1。介于两者之间的其他层称为隐藏层。
int numLayers = 4, lSz[4] = {3,3,3,1};
double beta = 0.2, alpha = 0.1, thresh = 0.00001;
long num_iter = 500000;创建网络
CBackProp *bp = new CBackProp(numLayers, lSz, beta, alpha);训练
for (long i=0; i < num_iter ; i++)
{
bp->bpgt(data[i%8], &data[i%8][3]);
if( bp->mse(&data[i%8][3]) < thresh)
break; // mse < threshold - we are done training!!!
}让我们测试它的智慧
我们准备测试数据,这与训练数据减去所需输出相同。
double testData[][3]={ // I XOR I XOR I = ?
//----------------------
0, 0, 0,
0, 0, 1,
0, 1, 0,
0, 1, 1,
1, 0, 0,
1, 0, 1,
1, 1, 0,
1, 1, 1};现在,使用经过训练的网络对我们的测试数据进行预测……
for ( i = 0 ; i < 8 ; i++ )
{
bp->ffwd(testData[i]);
cout << testData[i][0]<< " "
<< testData[i][1]<< " "
<< testData[i][2]<< " "
<< bp->Out(0) << endl;
}现在看看里面
神经网络的存储
我认为以下代码有足够的注释并且是不言自明的……
class CBackProp{
// output of each neuron
double **out;
// delta error value for each neuron
double **delta;
// 3-D array to store weights for each neuron
double ***weight;
// no of layers in net including input layer
int numl;
// array of numl elements to store size of each layer
int *lsize;
// learning rate
double beta;
// momentum
double alpha;
// storage for weight-change made in previous epoch
double ***prevDwt;
// sigmoid function
double sigmoid(double in);
public:
~CBackProp();
// initializes and allocates memory
CBackProp(int nl,int *sz,double b,double a);
// backpropogates error for one set of input
void bpgt(double *in,double *tgt);
// feed forwards activations for one set of inputs
void ffwd(double *in);
// returns mean square error of the net
double mse(double *tgt);
// returns i'th output of the net
double Out(int i) const;
};一些替代实现为层/神经元/连接定义了一个单独的类,然后将它们放在一起形成一个神经网络。尽管这绝对是一种更清洁的方法,但我决定通过分配所需的确切内存量来使用double ***并double **存储权重和输出等,原因是:
- 它在实现学习算法时提供的便利性,例如,对于第 (i-1)层的第 j个神经元和第 i层的第 k个神经元之间的连接权重,我个人更喜欢
w[i][k][j](而不是类似的东西net.layer[i].neuron[k].getWeight(j))。th第jth层的第 i 个神经元的输出是out[i][j],以此类推。 - 我觉得的另一个优点是可以灵活地选择任意数量和大小的层。
// initializes and allocates memory
CBackProp::CBackProp(int nl,int *sz,double b,double a):beta(b),alpha(a)
{
// Note that the following are unused,
//
// delta[0]
// weight[0]
// prevDwt[0]
// I did this intentionally to maintain
// consistency in numbering the layers.
// Since for a net having n layers,
// input layer is referred to as 0th layer,
// first hidden layer as 1st layer
// and the nth layer as output layer. And
// first (0th) layer just stores the inputs
// hence there is no delta or weight
// values associated to it.
// set no of layers and their sizes
numl=nl;
lsize=new int[numl];
for(int i=0;i<numl;i++){
lsize[i]=sz[i];
}
// allocate memory for output of each neuron
out = new double*[numl];
for( i=0;i<numl;i++){
out[i]=new double[lsize[i]];
}
// allocate memory for delta
delta = new double*[numl];
for(i=1;i<numl;i++){
delta[i]=new double[lsize[i]];
}
// allocate memory for weights
weight = new double**[numl];
for(i=1;i<numl;i++){
weight[i]=new double*[lsize[i]];
}
for(i=1;i<numl;i++){
for(int j=0;j<lsize[i];j++){
weight[i][j]=new double[lsize[i-1]+1];
}
}
// allocate memory for previous weights
prevDwt = new double**[numl];
for(i=1;i<numl;i++){
prevDwt[i]=new double*[lsize[i]];
}
for(i=1;i<numl;i++){
for(int j=0;j<lsize[i];j++){
prevDwt[i][j]=new double[lsize[i-1]+1];
}
}
// seed and assign random weights
srand((unsigned)(time(NULL)));
for(i=1;i<numl;i++)
for(int j=0;j<lsize[i];j++)
for(int k=0;k<lsize[i-1]+1;k++)
weight[i][j][k]=(double)(rand())/(RAND_MAX/2) - 1;
// initialize previous weights to 0 for first iteration
for(i=1;i<numl;i++)
for(int j=0;j<lsize[i];j++)
for(int k=0;k<lsize[i-1]+1;k++)
prevDwt[i][j][k]=(double)0.0;
}前馈
此函数更新每个神经元的输出值。从第一个隐藏层开始,它获取每个神经元的输入并o通过首先计算输入的加权和然后对其应用 Sigmoid 函数来找到输出 ( ),然后将其传递到下一层,直到输出层更新:
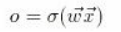
在哪里:
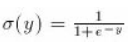
// feed forward one set of input
void CBackProp::ffwd(double *in)
{
double sum;
// assign content to input layer
for(int i=0;i < lsize[0];i++)
out[0][i]=in[i];
// assign output(activation) value
// to each neuron using sigmoid func
// For each layer
for(i=1;i < numl;i++){
// For each neuron in current layer
for(int j=0;j < lsize[i];j++){
sum=0.0;
// For input from each neuron in preceding layer
for(int k=0;k < lsize[i-1];k++){
// Apply weight to inputs and add to sum
sum+= out[i-1][k]*weight[i][j][k];
}
// Apply bias
sum+=weight[i][j][lsize[i-1]];
// Apply sigmoid function
out[i][j]=sigmoid(sum);
}
}
}反向传播…
该算法在函数中实现void CBackProp::bpgt(double *in,double *tgt)。以下是将输出层中的误差反向传播到第一个隐藏层所涉及的各个步骤。
void CBackProp::bpgt(double *in,double *tgt)
{
double sum;首先,我们调用void CBackProp::ffwd(double *in)更新每个神经元的输出值。此函数将输入输入到网络并找到每个神经元的输出:
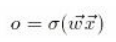
在哪里:
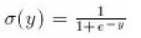
ffwd(in);下一步是找到输出层的增量:
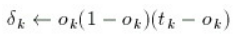
for(int i=0;i < lsize[numl-1];i++){
delta[numl-1][i]=out[numl-1][i]*
(1-out[numl-1][i])*(tgt[i]-out[numl-1][i]);
}然后找到隐藏层的增量…
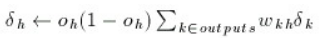
for(i=numl-2;i>0;i--){
for(int j=0;j < lsize[i];j++){
sum=0.0;
for(int k=0;k < lsize[i+1];k++){
sum+=delta[i+1][k]*weight[i+1][k][j];
}
delta[i][j]=out[i][j]*(1-out[i][j])*sum;
}
}应用动量(如果 alpha=0,则不执行任何操作):
for(i=1;i < numl;i++){
for(int j=0;j < lsize[i];j++){
for(int k=0;k < lsize[i-1];k++){
weight[i][j][k]+=alpha*prevDwt[i][j][k];
}
weight[i][j][lsize[i-1]]+=alpha*prevDwt[i][j][lsize[i-1]];
}
}最后,通过找到权重的修正来调整权重。
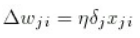
然后应用更正:
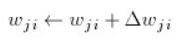
for(i=1;i < numl;i++){
for(int j=0;j < lsize[i];j++){
for(int k=0;k < lsize[i-1];k++){
prevDwt[i][j][k]=beta*delta[i][j]*out[i-1][k];
weight[i][j][k]+=prevDwt[i][j][k];
}
prevDwt[i][j][lsize[i-1]]=beta*delta[i][j];
weight[i][j][lsize[i-1]]+=prevDwt[i][j][lsize[i-1]];
}
}网络是如何学习的?
均方误差用于衡量神经网络的学习效果。
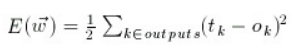
如示例 XOR 程序所示,我们应用上述步骤,直到达到令人满意的低错误水平。CBackProp::double mse(double *tgt)只是返回。