任务描述:
给你一个k链表数组lists,每个链表按升序排序。
将所有链表合并为一个排序的链表并返回。
示例 1:
Input: lists = [[1,4,5],[1,3,4],[2,6]]
Output: [1,1,2,3,4,4,5,6]
Explanation: The linked-lists are:
[
1->4->5,
1->3->4,
2->6
]
merging them into one sorted list:
1->1->2->3->4->4->5->6
解决方案:
在跳到这个问题的解决方案之前,让我们回顾一下链表是什么。

链表是由两个(双链表)指针中的一个(单链表)相互连接的节点组成的数据结构。每个节点通常包含一些值和指向下一个节点的指针。第一个节点称为 Head,最后一个节点称为 Tail。作为下一个指针的尾通常为空。
在这个任务中,我们正在处理排序的链表。这意味着每个节点中的所有值都已排序。每个列表中的每个节点的值都小于或等于它指向的节点中的值。为了形象化,这里有一个排序链表的例子。

了解排序链表是什么,我们可以解决问题的更简单版本。您将如何合并 2 个已排序的链表?
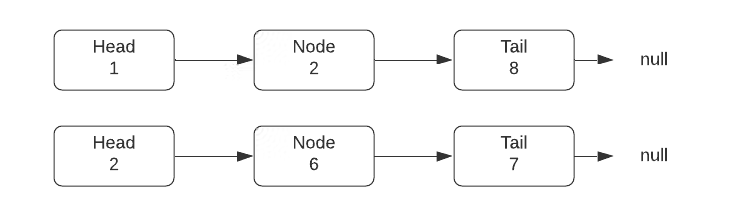
答案是——非常简单。比较每个列表的头部。选择具有最小值的节点。将其附加到您的答案中,并将指针调整到您从中挑选出一个节点的列表中的下一个节点。这样做直到其中一个头不等于空。一旦达到这一点,您就可以简单地将其余部分附加到您的答案中。
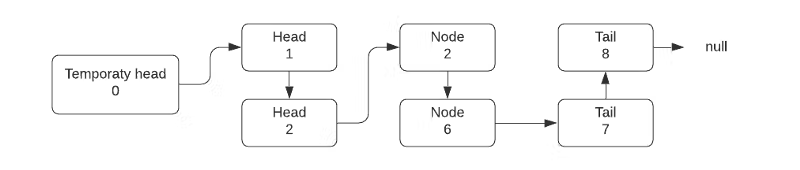
现在我们接近解决实际问题了。从更简单的任务中,我们看到解决方案的关键 – 获取具有最小值的节点并通过调整指针将其附加到答案。
拥有一个由 K 个排序的列表头组成的数组,我们可以遍历它并每次选择一个具有最小值的节点。它可以解决问题,但时间复杂度很糟糕。
更好的方法是获取每个列表的头部并将其添加到优先级队列中。Priority Queue 是另一种数据结构,可在 O(1) 恒定时间内提供最小或最大值。并在 O(log n) 时间内添加或删除这个值,这对我们的任务来说已经足够了。根据存储元素的方式,优先级队列通常称为二叉堆。我可以在以后的文章中描述它。
public ListNode mergeKLists(ListNode[] lists)
{
if (lists == null || lists.length == 0)
{
return null;
}
ListNode dummy = new ListNode(0);
ListNode prev = dummy;
ListNode current;
ListNode next;
PriorityQueue<ListNode> minHeap = new PriorityQueue<>(
Comparator.comparingInt(head -> head.val)
);
for (ListNode node : lists)
{
if (node != null)
{
minHeap.add(node);
}
}
while (!minHeap.isEmpty())
{
current = minHeap.remove();
if (current == null)
{
continue;
}
next = current.next;
current.next = null;
prev.next = current;
prev = current;
if (next != null)
{
minHeap.add(next);
}
}
return dummy.next;
}
在第 8 行中,我们创建了一个“虚拟”节点,作为我们的临时头。它将帮助我们通过调用 dummy.next 轻松返回排序链表的真实头部
在第 13-15 行,我们创建了一个优先队列。我们需要对其中的元素进行排序。为此,我们提供了比较器。
在第 17-23 行,我们将所有非空头添加到优先级队列中。
在第 25-42 行,我们有一个包含主逻辑的主 while 循环。
我们通过从优先级队列顶部删除具有最小值的节点来更新当前节点。然后我们通过从当前节点获取下一个节点来更新下一个指针。我们还需要更新 prev 指针。您可以将 prev 指针视为指向我们正在构建的链表的临时尾部的指针。最后但同样重要的是,如果下一个链接不为空,我们必须将其推回优先级队列。
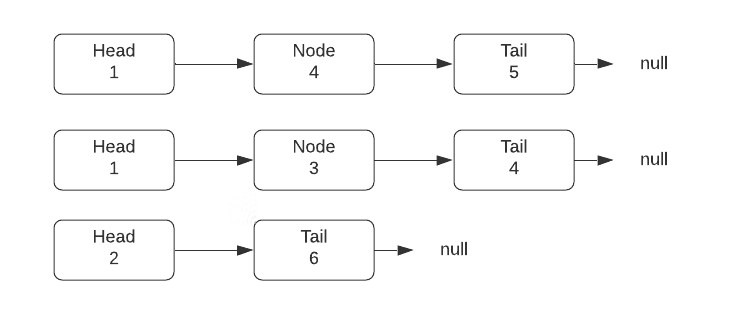
执行给定示例 1 中的前面步骤后,我们将获得如下所示的状态。我故意没有把它弄平。向您展示从原始状态到最终状态的转换
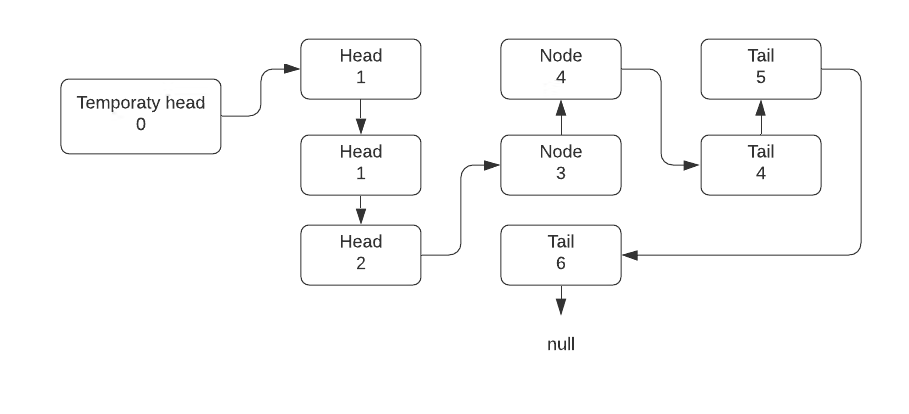
上面列出的算法为我们提供了以下结果。

我们的解决方案的时间复杂度是 O(N log K),其中 N – 是所有列表中的节点总数,其中 K – 是我们拥有的已排序链表的数量。
我们的解决方案的空间复杂度是 O(N),其中 N – 是创建答案的节点总数加上 O(K),其中 K – 是我们拥有的已排序链表的数量。根据大 O 表示法,我们可以省略 O(K),因为就元素数量而言,它可能等于或小于 O(N)。